本文为清华-康奈尔双学位金融MBA2017级“数据分析与创业决策”课后作业,作者是学生第七小组,成员包括谢晨曦、郑明贺、何川等同学。授课教师:余剑峰(清华大学五道口金融学院建树金融学讲席教授,清华大学国家金融研究院资产管理研究中心主任)。
现象描述
在康奈尔的高级会计课上,Sanjeev Bhojaj教授给我们展示了一个有趣的实证研究结果,根据Nissim和Penman(2001),以及Halsey(2010)的实证分析,得出以下结论:
在该实证研究中ROA= (Net Income + Interest Expense × ( 1-t ) )/ Total Assets,可以用杜邦分析分解为Profit Margin ×总资产周转率 = (Net Income +Interest Expense × ( 1-t ) )/Sales× Sales / Total Assets,其中ProfitMargin简称为PM,总资产周转率简称为ATO,因而PM和ATO在杜邦分析中呈反函数形态。
图1:1995-2005 PM与ATO分行业分布
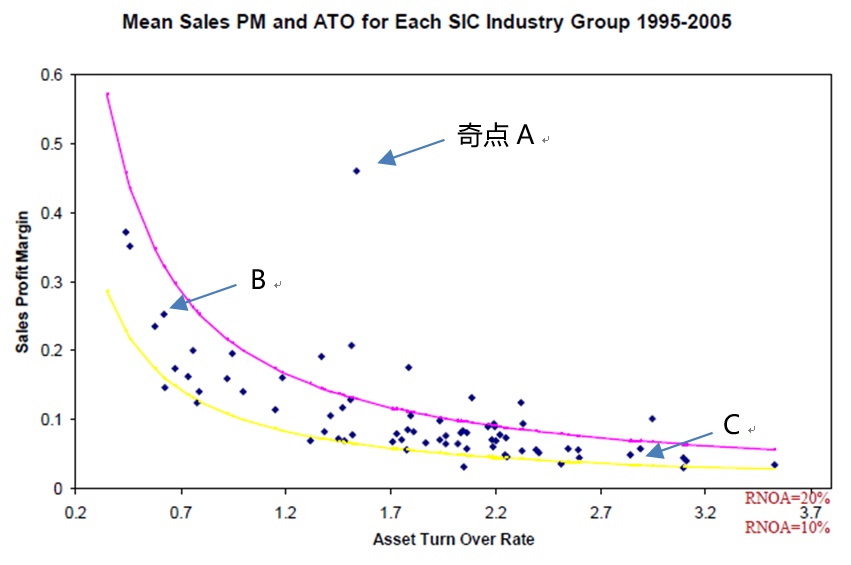
图1展示了1995年至2005年各行业的PM和ATO关系,其乘积结果即ROA,集中分布在10%-20%之间。经济学或会计学解释是,不同行业的商业模式不同,PM高的行业,ATO必然低,反过来ATO高的,PM必然低。例如精密仪器制造商,因产品附加值高,且具有很高的行业壁垒,PM会包含专利和特殊价值而会很高,但因为市场空间和销售难度等原因ATO相对较低,如图1中的点B;而超市则属于薄利多销型,通过快速的资产周转ATO,卖出货品,赚取多次资产周转带来的相对较低的PM,如图1中的点C。
而有趣的是图1中的奇点A,A点为烟草行业。因为较高的行业壁垒和准入,以及实际垄断的行业特征,烟草行业得以同时获得较高的PM和ATO,最终获得高于全市场平均的ROA。而这个行业不可能永远获得超额的ROA回报,根据时间序列分析,所有的ROA都服从一个回归平均的趋势,如图2所示。最终烟草行业的奇点A,都会回归到行业的平均范围区间内,理由是超额收益会带来更多的竞争。而烟草行业因垄断获得了政府的特别关注,征收了更高的税负和更多的运营限制。
图2:1995-2005RNOA的时间序列分析
这个结果非常有趣,我们好奇如果某些行业能够成为超过市场的ROA平均值,那是否存在超过市场平均的ROA个股,这些个股的表现是否能够超过市场平均?如果存在,这些股票是否可以形成投资策略或机会。
实证研究方法、过程和结果
我们通过万得数据库,下载了截止2018年5月16日A股的3517支股票的2015-2017三年的杜邦分析的PM和ATO的数据。Wind对PM的定义略有不同是EBIT/Sales而不是净利润+税盾,ATO的定义为Sales/Average Total Assets,但这不影响我们最后的结果。
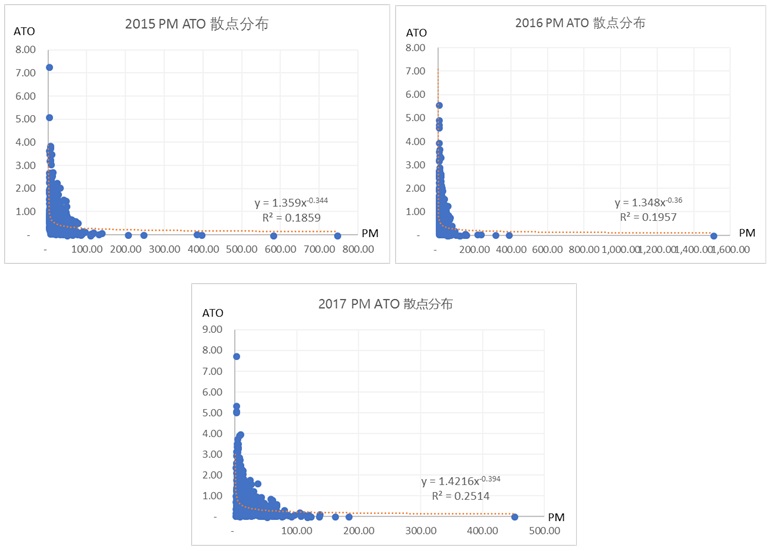
数据样例如表1所示,所采数据样本的散点分布如图3-图5所示。散点分布纵轴为ATO,横轴为PM,2017年的回归方程为y = 1.4216x-0.394 ,R² = 0.2514,2016年为y = 1.348x-0.36,R² = 0.1957,2015年为y= 1.359x-0.344,R² = 0.1859,大致符合原研究反函数的形态。
表1: 3517支股票2015-2017PM和ATO数据示例
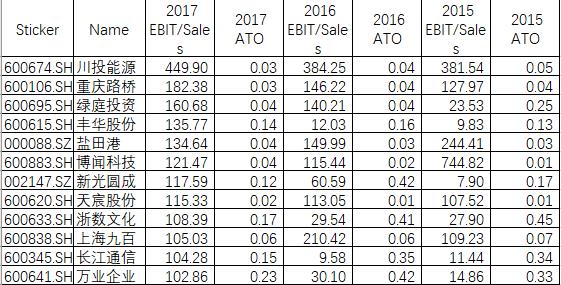
图3-5 2015-2017年PM和ATO散点分布图
我们想对3517个样本用excel做回归分析,但受以下条件约束:
1. excel只能做线性一次方程,所以我们需要对PM或ATO做非线性变换,因反函数是单调函数,非线性变化并不影响最后的结果。
2. ATO本身的变化值较小,非线性变换后,结果范围会比PM的小,所以我们选择对ATO做一下反函数变换,即1/ATO。
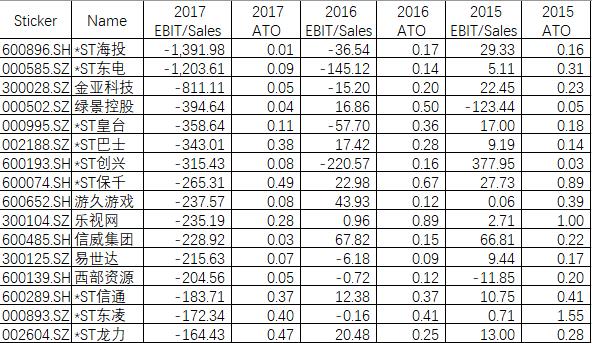
3.PM为负数或无数据的点无法在excel中做回归,对这些点做剔除。经济学上也能够做相应解释,如果企业EBIT都为负,市场应该对其进行相对折价,股价表现也不应该比市场更优,也不是我们选股的标准,如图2所示很多剔除的标的为*ST股票。而无PM或ATO数据的点为金融行业公司,这是因万得对EBIT的定义和杜邦分析对金融公司不适用,这个部分需要未来研究改进。删除的样本案例如表2,样本点共658家。
表2:剔除无法回归的样本示例
我们关心这些选出的ROA样本是否也有回归均值的趋势呢?我们将2015-2017年各年的PM和ATO相乘得到个股的ROA,再将2860个样本点对分时间进行双样本异方差假设t检验,结果如表3所示:
表3:2015-2017年ROA t检验结果
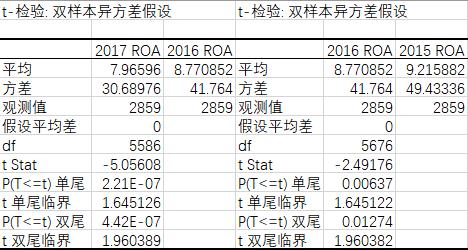
根据结果,2017年的平均ROA显著低于2016年(t-Stat=-5.05608),2017年的平均ROA显著低于2015年(t-Stat= -2.49176)。再次印证了Nissim和Penman(2001),以及Halsey(2010)的实证结果。
接下来我们用2015-2017年间每年的PM和1/ATO做回归分析,即PMn=a+b/ATOn。得出结果如下,以2017年结果为例:
表4:2017年回归分析结果
2017年的回归方程为 PM2017 = 7.4695 + 3.5500 / ATO2017
(22.8651) (38.6492) 截距和斜率估计均显著。
根据之前的推测和猜想,我们想选出的股票是回归置信区间外的奇点,如图6所示。选择的标准为在所有99%置信区间上限外的点,即同时在这三条约束范围之外的股票:
1. PM2017=8.3115 + 3.5500/ ATO2017,
2. PM2017=7.4695+ 3.7867 /ATO2017,
3. PM2017=8.3115 + 3.7867/ ATO2017,
经济学逻辑为,PM和1/ATO相乘乘积要高于回归分析的置信区间和行业平均,则只可能在置信区间的上限而不是下限。
图6:置信区间外的奇点的选择
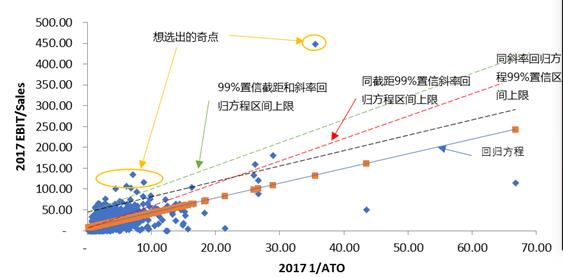
根据计算,选择出满足约束条件的奇点,并将三年均属于奇点的股票选择出来。选择的经济学逻辑是,ROA的回归平均水平是一个长时间过程,市场很难是完全竞争市场,任何的超额收益的回归都需要时间调整,所以选择三年ROA都是奇点的样本做整体检验是否显著比单年的稳定一些。选出的样本点如表5所示:
表5:置信区间外的点的选择样本示例
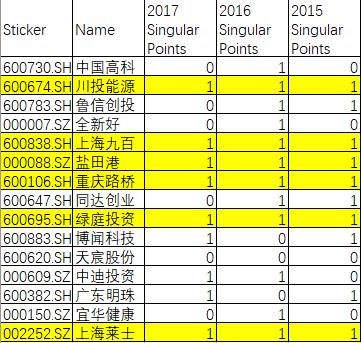
按照三年均满足奇点的要求,剔除了2147个样本点,剩余713样本点/股票,其中主板285只,中小板200只,创业板228只。接下来验证选出来的713只股票是否能较市场获得超额收益。
表6:对应板块指数涨跌幅
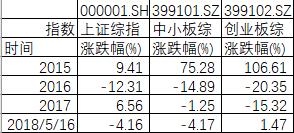
表7:选出的主板股票市场表现示例
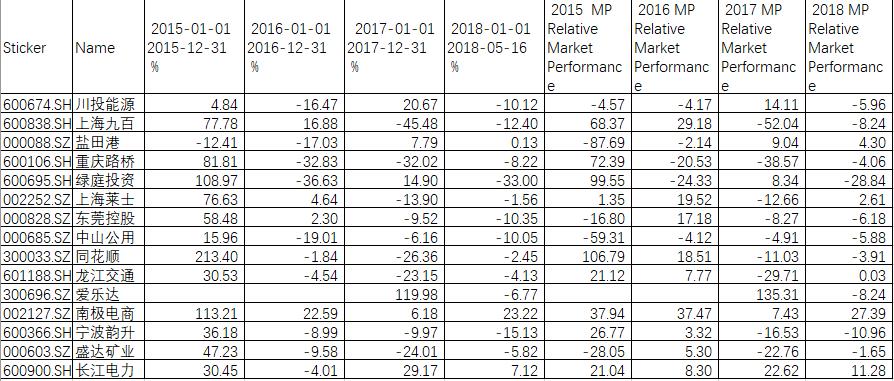
如表6和表7所示,我们将选出的股票对应的年份的表现与对应板块的涨跌幅相减,得出样本区间相较于大盘的涨跌幅数据。例如,主板的重庆路桥2015年涨幅81.81%,对应大盘是上证综指2015年涨幅9.41%,相对收益为81.81%-9.41%=72.39%,同理可得2016年为-32.83% - (-12.31%)=-20.53%,2017年-32.02%-6.56%=-38.57%,2018年-8.22%-(-4.16%)=-4.06%。而中小板和创业板的股票,则减去对应的中小板综指和创业板综指。图中如区间无涨跌幅数据,则可能为还未上市,或存在当年停牌等情况。
假设将基金分为金额相等的713份,每份持有选出的713只股票,形成的资产组合与对应大盘的指数进行对比。样本的收益统计结果以创业板数据展示如下表8。对于当年没有涨跌幅数据的股票没有纳入统计范围。
表8:选出的创业板奇点超市场预期统计样本分析
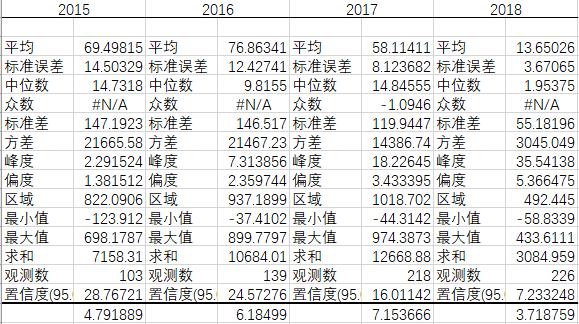
可以看出,2015年,创业板的229个样本点分别在2015-2018年获得超出同期板块69.49%,76.86%,58.11%和13.65%的超额收益(abnormal return)。
且根据t假设检验,H0: R=0,H1:R≠0。构造t假设检验估计:
t=R / stdev ×sqrt(n-1)
算出t值均远远大于1.96,可以得出这些超额收益(abnormal return)显著大于0的结论,即选出的股票均可获得比大盘更高的收益。而这个结果在主板和中小板的样本中也得到了相同的应证。
该结果与经典的EMH有所冲突,根据EMH理论,股票的所有信息都包含在了股票价格中,市场对于股票的分析和判断完整而无偏,所以没有股票能够获得长期的超过市场的超额收益。但我们根据ROA的特性,选出了三年均在市场更高ROA水平的公司股票,并将他们等额持有,结果显示每年我们均可以获得显著超过市场的收益,验证了我们开始的猜想,那如何将这个猜想变为投资策略呢。
ROA数据仅在每个会计年度结束后才能获得,暂时不考虑公告时间差的因素,如何将这个特性转换为股票选择的策略,获得超过市场的收益是我们关注的重点。
策略1:假设年初获得去年的PM和ATO信息,决定今年是否要持有该股票年底卖出。
今年决定投资的股票的组合是否能够打败同期没有被选择的股票呢?
表9:策略一,去年决定今年的选择,t检验
利用之前表7算出的相对市场表现,按照相同的选择奇点的标准,从2015年选出了ROA高于回归置信区间99%的716个样本点,将其与2016年没有被选择的样本比较,收益高出21.51% (41.46%-19.95%,t-stat: 4.98)。同理2017, 2018年比同期的其他样本要高出31.69%(t-stat 9.07)和9.92%(t-stat: 7.44)。检验显示策略1有效,即每年年初选择上一年ROA的奇点,并等份额组合持有,获得的超额收益率41.46%。
策略2:每年购买去年的奇点,并持有。每年年初根据上一年的ROA奇点的判定,选择是否要持有该股票,如果是奇点,则将等额资金投入到这些股票中,如果不是,则不买入,或卖掉过去持有的份额,重新等额买入其他股票。
表10:策略二买入并持有,t检验
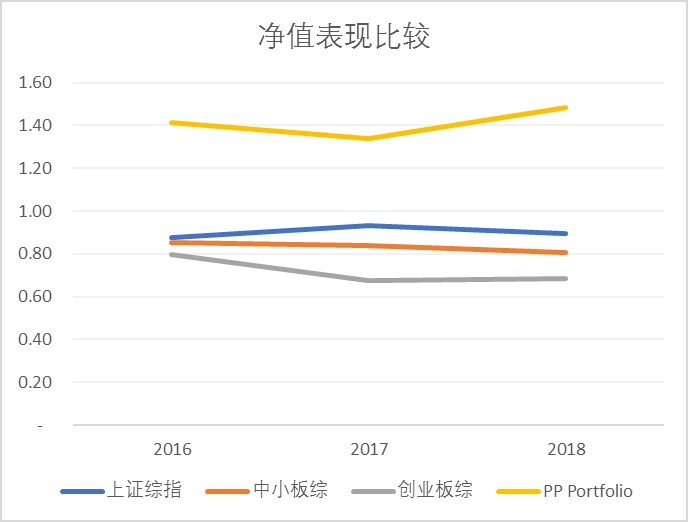
同样利用表7中算出的超额收益计算,如果从2016年1月1日开始持有2015年选出的716个奇点100万元,获得超额收益41.46%,年末价值为141.46万元。2017年1月1日再进行一次判定,如果还是就继续持有,如果不是就卖掉,如果有新的奇点则开始持有,新的514个样本组合,获得超额收益-5.24%,年末组合变为134.05万元。2018年年初再判定,2017年这些样本是否还是奇点,是则继续持有,如果不是则卖出,如果为新奇点则买入,400个样本组合获得了10.50%的投资收益,变为148.13万元。而对应的板块指数收益如表11所示,2016年年初投资100万元,则上证综指年末88万元,2017年底93万元,2018年5月变为90万元。
表11:策略二表现与大盘比较

图7:策略二组合净值与大盘表现比较
 案例分析和解释
案例分析和解释
以主板的贵州茅台为例,该公司成立于1999年,于2001年在上海证券交易所上市。根据我们2015,2016和2017年三年的数据分析,该公司三年均为奇点,且在2015年收益率比主板市场同期高19.4%,2016年高68.76%,2017年高出105.33,近三年比主板市场收益率高出50%以上。我们进一步选取了主板制造业的白酒行业作为分析,贵州茅台在EBIT/SALES的数值上三年来远远高于行业平均值,其ATO低于行业平均值。
贵州茅台在2015到2017年均获得了超额市场收益,我们选取古越龙山进行对比,该股票在三年内均未获得超额市场收益,且三年均未成为奇点。其可能原因如下:
表12:贵州茅台和其他酒类对比

1. 财务原因
从财务上分析,对比贵州茅台和古越龙山,贵州茅台的净利润率和净资产收益率大大高于古越龙山,其财务上表现优异是其能够获得市场超额收益的原因之一。
图8.贵州茅台和古越龙山净利润率对比
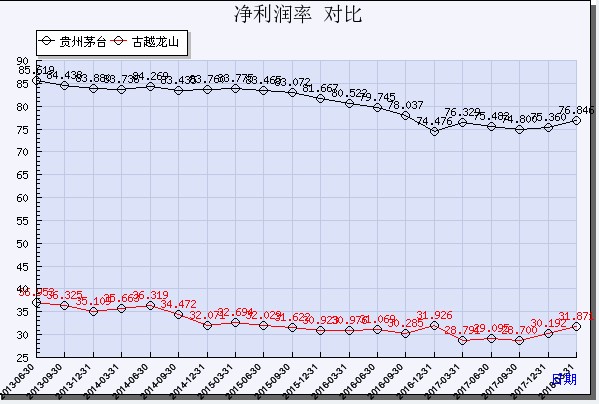
图9.贵州茅台和古越龙山净资产收益率对比
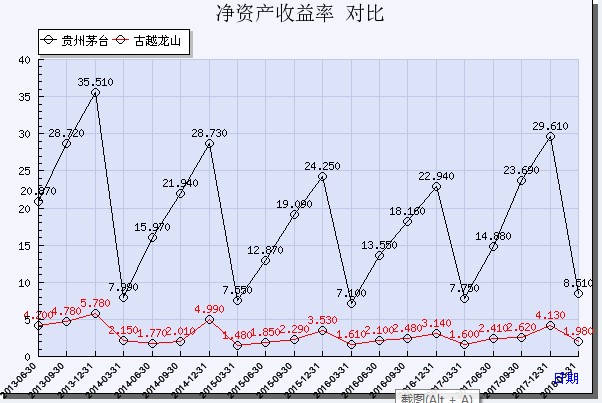
表13.贵州茅台和古月龙山财务数据对比
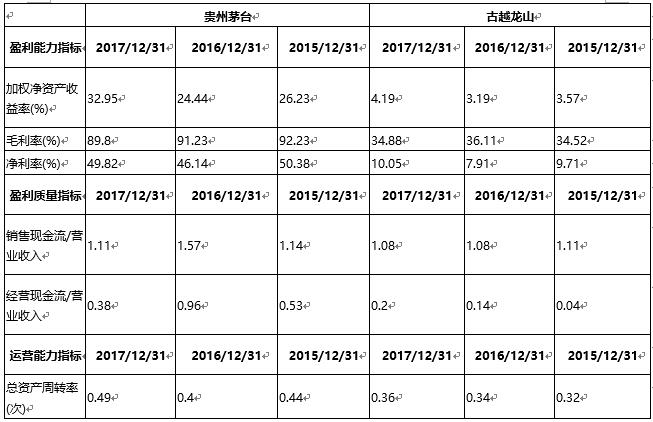
从两家公司详细财务数据对比上,贵州茅台在毛利率和净利率等盈利指标明显高于古越龙山,此外茅台的销售现金流/营业收入与经营现金流/营业收入指标明显好于古越龙山。最后,其茅台在总资产周转率上也高于古越龙山。
2. 白酒具有快速消费品的属性,茅台的需求没有绝对饱和,茅台价格下降后(零售价格逐渐降到1000元以下),其需求迅速增加,导致其财务状况变好。
3. 茅台作为一流龙头企业,具有品牌优势、品质优势和市场贵广优势,该品牌积压了其他白酒品牌,从而使得茅台在稳定经营的基础上可以适度成长。
可以看出ROA奇点选择可以作为快速筛选合适股票的一个手段,辅助基本面分析,选出可以获得超额收益股票的一个策略。
本研究分析的不足
1. 因时间和资源限制,本研究仅针对了2015-2017三年的A股针对杜邦分析的PM和1/ATO进行了回归分析,时间跨度不够长,对于EMH的反驳力度不够大。
2. 本研究的回归分析没有对行业进行区分,泛行业的PM和1/ATO的回归分析可能将某些行业内的更有代表性或特点的奇点给抹除。
3. 对样本的非线性处理可能存在拟合度更优的处理,如对数,指数,乘数等。
4. 删除的658个样本中,因万得对金融行业的EBIT定义不同,导致金融行业的样本全部被删除,对策略的结果可能会产生影响。
5. 因为年报公布的时间有差异,不可能再年初获得,一般是在一季度结束之后,所以本研究有待细化到季度,并考虑季节因素。
6. 选股策略还可以根据其他信号进一步优化,配合基本面分析获得更小组合更优收益。
参考文献
1. DoronNissim, Stephen H. Penman, 2001, Ratio Analysis and Equity Valuation: From Research to Practice, Review of Accounting Studies, 6, 109-154.
2. RobertHalsey, 2010, Reversion of RNOA and itsComponents, Babson Faculty Research Fund Working Papers, Paper 72.

